[C++] Genetic Algorithm
You can find the coding example here on compiler explorer.
Even it's still November, I set myself a new year resolution: Learning and understanding artificial intelligence. And therefore I'll start in this article with the genetic algorithm.
Theory
I don't want to write to much about the theory behind the algorithm, because there are plenty of articles and videos online available. But to cover the basic ideo of the genetic algorithm consider the following:
The genetic algorithm belongs to search algorithms. We have a defined target to find and we know what it is. We create random values, called individuals and all individuals belong to a population. Each individual holds a value which can be our value to find. And like nature does, a population changes or evolves. This means in short:
- Initialize a population (first generation)
- Calculate their fitness (the fitness will tell how close we're to our target)
- Find the strongest individuals
- Cross Individuals And Create A New Population (some individuals we create from existing ones, some are entirely new)
- Mutate individuals (this means values are changing with a slight probability)
- Go back to 2. until we find our target
In our example we want to find a string value: coding_with_thomas. This means each individual is a string. So let's go through this by example.
1. Initialize Random Population - 1. Generation
This is now the first generation of our population, where I illustrate three random strings here:
And notice the green highilighted squares, by assigning random values we have some hits already.
2. Calculate Their Fitness
Now we need to calculate the strength or fitness of each individual. The fitness value will give the sorting order later and is calculated by the number of matching characters to our target. Consider the pseudo code here:
// pseudo code:
string target = "coding_with_thomas"
int target_size = target.size()
class individual {
string individual_string = "5o$TnG91vh+}n!xT20"
int fitness = 0
void calculate_fitness() {
for (int i = 0 ; i < target_size ; i++) {
if (individual_string[i] == target[i]) {
fitness++
}
}
}
}3. Select The Strongest Individuals
With our given Strings we'll drop the first, because there was only one match. These two will be later our Parents.
4. Cross The Parents And Generate New Population
Now we cross the two parents to create a child, later in the code you'll find random probability of how much characters do we take from Parent 1 and how much characters do we take from Parent 2.
In this illustration we only considering the strongest individuals, but the crossover ratio refers to the entire population
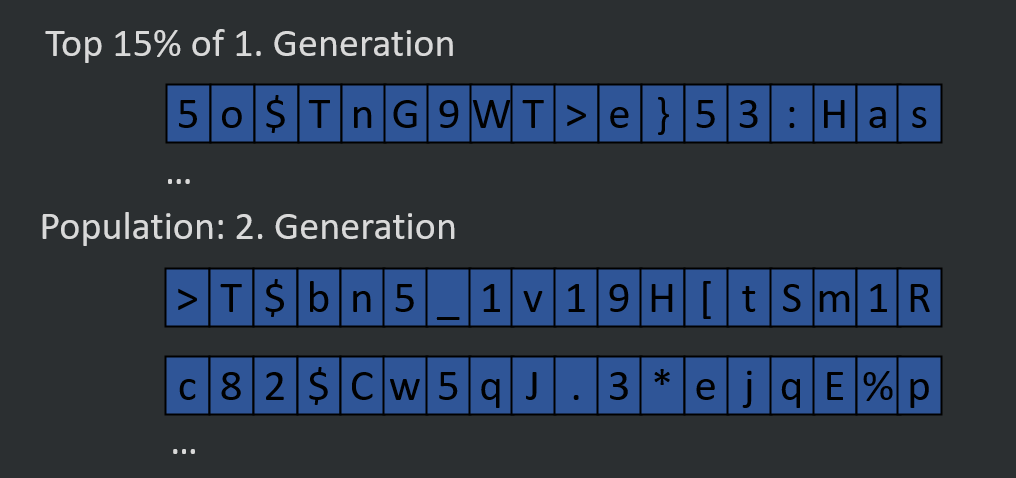
We take the childs from the strongest parents. In the example we'll see way more childs. We determine a threshold of how many childs we want to take into our next generation, like the strongest 15%.
Now we have on top the strongest “survivors” from the 1. Generation and create the 2. Generation
5. Mutate Childs
Like in real evolution, it can be the case that childs mutate. This means some childs are changing values. In the code you'll also find a random probability to do so.
Our child just mutated. Can be good or not, evolution decides …
6. Calculate The Fitness And Start Over
Now we are iterating over each individual in our Generation, calculate their fitness, determine the strongest, creating their childs, mutate them and do this over and over again until we've found our string. This means we're going back to 3.
And now, we'll implement the algorithm.
C++ Implementation
In our implementation we'll create two classes, an individual and the population. Let's start with the individual:
// an individual will represent a string value with their corresponding fitness
class individual {
public:
// one constructor to initialize a random individual
// both constructors calculate the fitness right away
// details::get_random_string is an helper function which creates (guess what)
// a random string, you can find the helper function in the example
individual() : m_value(details::get_random_string(target.size())), m_fitness(0) {
calculate_fitness();
}
// one constructor where we already have a string value to an individual
individual(const std::string& value) : m_value(value), m_fitness(0) {
calculate_fitness();
}
// some getters
std::string get_value() const {
return m_value;
}
std::size_t get_fitness() const {
return m_fitness;
}
// the square bracket overload to access single characters in our string
auto operator[](const int i) const {
return m_value[i];
}
// the greater operator overload to sort the values later
bool operator > (const individual& rhs) const {
return (m_fitness > rhs.m_fitness);
}
private:
// the fitness is calculated here
// the more characters match our target the higher the fitness value is
void calculate_fitness() {
for (int i = 0 ; i < target.size() ; i++) {
if (target[i] == m_value[i]) {
m_fitness++;
}
}
}
private:
std::string m_value;
std::size_t m_fitness;
};And now we hold all individuals in population:
class population
{
public:
// population constructors where we pass all values which we need
// all ratios and probabilities are given in integer percentage values 0..100
// and absolute values are calculated here in the constructor
population(const std::size_t max_population, const std::size_t parent_ratio, const std::size_t mutate_probability, const std::size_t transfer_ratio, const std::size_t crossover)
: m_generation{1}, m_parent_ratio{parent_ratio}, m_mutate_probability{mutate_probability}
{
// how many individuals we take to the next generation
m_transfer_count = (transfer_ratio*max_population)/100;
// 0..m_crossover_threshold determines the parents in our population
m_crossover_threshold = (crossover*max_population)/100;
// m_new_individuals_per_generation is the number of new created individuals
// in a next generation
m_new_individuals_per_generation = max_population-m_transfer_count;
// reserve some storage already in our vector since we know the population size
m_population.reserve(max_population);
// generate random individuals in our population
std::generate_n(std::back_inserter(m_population), max_population, [](){ return individual{}; });
// and sort them
this->sort();
}
std::size_t get_generation() const {
return m_generation;
}
// just use std::sort to get decending order of individuals
void sort() {
std::sort(std::begin(m_population), std::end(m_population), [](const auto& left, const auto& right){ return left > right;});
}
// this will create a new generation
void create_next_generation() {
// increment generation counter
m_generation++;
// create a tmp vector which represents the new generation
std::vector<individual> next_generation;
next_generation.reserve(m_population.size());
// push the best individuals in our next generation
for (std::size_t i = 0 ; i < m_transfer_count ; i++) {
next_generation.push_back(m_population[i]);
}
// create the crossover individuals
for (std::size_t i = 0 ; i < m_new_individuals_per_generation ; i++) {
// the mother is any individual between 0..m_crossover_threshold
individual& mother = this->m_population[details::get_random_number(0,m_crossover_threshold)];
// same for the father
individual& father = this->m_population[details::get_random_number(0,m_crossover_threshold)];
// and push the new created child to the new generation
// the helper function is described below
next_generation.push_back(create_child(mother, father, m_parent_ratio, m_mutate_probability));
}
// overwrite our population with the new created one
m_population = next_generation;
}
const individual& front() const {
return m_population.front();
}
private:
std::vector<individual> m_population;
std::size_t m_generation;
std::size_t m_parent_ratio;
std::size_t m_mutate_probability;
std::size_t m_transfer_count;
std::size_t m_crossover_threshold;
std::size_t m_new_individuals_per_generation;
};
And finally let's see how new childs are created:
// we'll return a new child from mother and father
// parent_ratio considers how much mother/father is "in the child"
// mutate_probability refers if a gene mutates
individual create_child(const individual& mother, const individual& father, const std::size_t parent_ratio, const std::size_t mutate_probability)
{
// initialize childs string value
std::string childs_value{""};
// iterate over all characters of the target size
for (int i = 0 ; i < target.size() ; i++)
{
// if the gene is about to mutate we append any character
if (details::get_random_number(0,100) < mutate_probability) {
childs_value += details::get_random_char();
// else we take either mothers or fahters character
} else if (details::get_random_number(0,100) < parent_ratio) {
childs_value += mother[i];
} else {
childs_value += father[i];
}
}
// return our new individual
return individual{childs_value};
}
And now we can use population like this to find coding_with_thomas:
int main()
{
// create random seeds for our random value fanctions
srand (time(NULL));
// variables we can adjust
const std::size_t population_size = 500;
const std::size_t parent_ratio = 50;
const std::size_t mutate_probability = 10;
const std::size_t transfer_ratio = 15;
const std::size_t crossover = 50;
// create our population in the first generation
cwt::population population(population_size, parent_ratio, mutate_probability, transfer_ratio, crossover);
// until we haven't found our target
// we continue to create a next generation and sort them
while(population.front().get_fitness() < target.size())
{
std::cout << population.get_generation() << " Generations best match: " << population.front().get_value() << std::endl;
population.create_next_generation();
population.sort();
}
std::cout << population.get_generation() << " Generations best match: " << population.front().get_value() << std::endl;
return 0;
}
Which now gives this output for example. Since their are used random values, you'll probably not get the same output.
1. Generations best match: BjqCwE5wI=u;tQo6({
2. Generations best match: BjqCwE5wI=u;tQo6({
3. Generations best match: c,9[[O{Stl}V"MomGB
4. Generations best match: No".23lw%tb_kUbqlg
5. Generations best match: No#.n3lw%tb_khQqG:
6. Generations best match: LH=Png9wfA)_ XOma9
7. Generations best match: coqCAA-wi hRthHdaC
8. Generations best match: c,dinOtwii@_tbo ({
9. Generations best match: c,dinOtwii@_tbo ({
10. Generations best match: coTinoRiuJb_thomVs
11. Generations best match: cozpnI]with_tAoma&
12. Generations best match: cozpnI]with_tAoma&
13. Generations best match: co8Mngywit{7thomas
14. Generations best match: coding$wivW_thoCay
15. Generations best match: codinI@w:th_thoma&
16. Generations best match: Noding_pitu_Dhomas
17. Generations best match: coding5aith_thomas
18. Generations best match: coting_wit3_thomas
19. Generations best match: coding}with_thomas
20. Generations best match: coding_with_rhomas
21. Generations best match: coding_with_thomasYou can find the coding example here on compiler explorer.
Conclusion
And that's it, that is the genetic algorithm with my string example. This is basically the same example from geeksforgeeks, but with my implementation here.
There other real world examples where this algorithm is used, but I really like this string search, because you can see what happens during the search. Also the child creation with their parents and mutation is quite understandable.
But that's it for now, I hope that helped.
Best Thomas